Opracowanie ankiety
Jak wykonać? Przykładowe opracowanie
Aby zademonstrować w jaki sposób wykonywana jest przez nas analiza ankiety, stworzyliśmy krótki, przykładowy kwestionariusz pytań. Problemem badawczym owego hipotetycznego sondażu, było sprawdzenie czy przyswajanie wiedzy z zakresu statystyki zależne jest od profilu klasy ucznia. Porównywano klasy o profilu humanistycznym i biologicznym. Interesowało nas również, czy opanowanie materiału było zależne od nauczyciela prowadzącego zajęcia matematyczne oraz czy zdolności matematyczne ucznia miały wpływ na jego zrozumienie tematu. Skonstruowaną do tego celu ankietę, możemy zobaczyć pod poniższym linkiem: przykładowa ankieta. Uzyskane wyniki przenieśliśmy do bazy danych, skonstruowanej według wymienionych przez nas wskazówek.
Analiza statystyczna badanej grupy
Zanim zaczniemy analizę stawianych przez nas hipotez, należy przyjrzeć się danym z metryczki. Dokładne jej opracowanie, ułatwia nam interpretację uzyskanych wyników. Dodatkowo w tym momencie możemy, dokonać ostatecznej korekty naszych wyników. Przykładowo korzystając z testu chi kwadrat nasze wartości oczekiwane muszą być większe od 5. Gdy tak nie jest możemy nasze zmienne rekodować, tak aby nasze wartości spełniały ten warunek. Przykładowo liczba osób w wieku od 10 do 18 lat wynosi 4, następna klasa to grupa osób od 18 do 25 lat i liczy ona 20 osób. W tej sytuacji lepiej zlikwidować pierwszą klasę, ale żeby nie utracić danych trzeba ją połączyć z drugą kategorią wiekową. Tworzymy nową grupę wiekową – poniżej 25 lat. Dlatego, każdy skonstruowany przez nas raport zaczynamy od opracowania metryki. Wróćmy jednak do opracowania naszej przykładowej ankiety.
W badaniu brało udział osiemdziesięciu uczniów jednego z ogólnokształcących liceum. Mężczyźni stanowili 57,5% ogółu. Dokładną strukturę płci przedstawiono na poniższym wykresie.

W analizie wzięło udział 48 uczniów o humanistycznym profilu klas (60% ogółu) oraz 32 uczniów z klas o profilu biologicznym (40% ogółu) (Ryc. 2). Sprawdzono rozkład płci w poszczególnych klasach. W klasach o profilu humanistycznym, uczyło się 20 kobiet oraz 28 mężczyzn, w klasach o profilu biologicznym było 14 kobiet oraz 18 - stu mężczyzn. Za pomocą testu chi kwadrat sprawdzono, czy klasy różniły się pod względem płci. Wartość testu wynosiła 0,034 przy poziomie istotności 0,853. Rozkład płci w obu profilach klas był do siebie zbliżony (Tab. 1).


Na uzyskany wyniki wpływ mógł mieć nie tylko profil klasy, ale również jaki nauczyciel prowadził zajęcia z matematyki. W badanym liceum, przedmiot prowadziło dwóch nauczycieli - pani mgr Anna Mediana oraz pani Zofia Chi Kwadrat. Nauczyciele uczyli podobną liczbę osób - pierwszy z nich miał do dyspozycji 41 uczniów, drugi 39 (Ryc. 3). Magister Anna Mediana uczyła zdecydowanie więcej humanistów niż biologów, magister Chi Kwadrat miała podobną liczbę uczniów z obu profili klasowych. Jednakże test chi kwadrat nie wykazał by rozkłady uczniów pomiędzy nauczycielami różniły się istotnie (2,41; p=0,121) (Tab. 2).
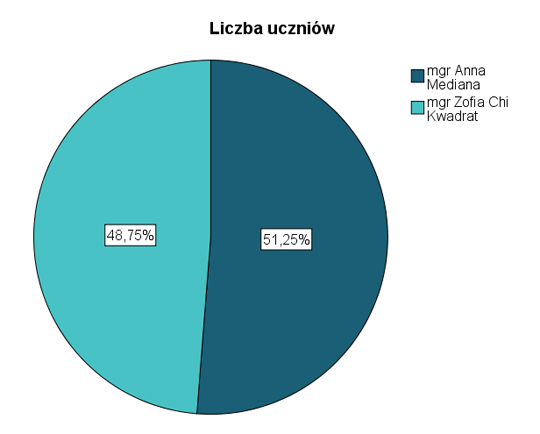
W tym przypadku zastosowaliśmy diagram kołowy. Jest to w naszych analizach ankiet, rzadko stosowana prezentacja danych . Jesteśmy zwolennikami wykresów słupkowych, jednakże czasem warto je zastosować dla uatrakcyjnienia wizualnej formy pracy.

Analiza statystyczna stawianych hipotez
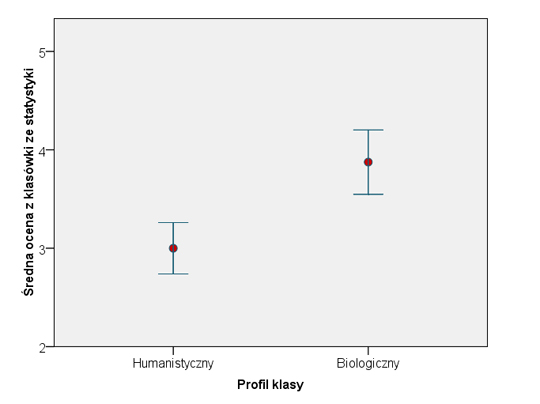
Średnia ocena z zajęć statystycznych uzyskana przez uczniów profilu humanistycznym wynosiła 3, przy odchyleniu standardowym 0,9. Minimalna uzyskana ocena to 2, najwyższa ocena to 5. Mediana ocen wynosi 3, moda również 3. Wykres ocen jest prawoskośny. Ocenę 4 lub wyższą uzyskało raptem 27% uczniów (ryc. 4). W przypadku uczniów profilu biologicznego, ponad 71% osób uzyskało ocenę wyższą niż 4. Najniższy stopień uzyskały tylko 3 osoby. Na ocenę 5 zasłużyło 8 uczniów. Średnia dla tej grupy wynosiła 3,88, przy odchyleniu 0,91. mediana rozkładu to 4, wartość modalna również 4, liczebność mody to 15 osób (ryc. 5). Rozkłady ocen zaprezentowano na poniższych wykresach:


Do weryfikacji pierwszej z hipotez, posłużono się nieparametrycznym testem U Manna - Whitneya. Nie wymaga on zgodności rozkładów z rozkładem normalnym. Wartość testu z wynosiła -3,89 przy poziomie istotności równym 0,000. Co pozwala odrzucić naszą hipotezę o równości średnich rang rozkładów. Rodzaj profilu do którego przynależał uczeń miał wpływ na uzyskane wyniki w klasówce ze statystyki. Humaniści uzyskiwali gorsze oceny, niż uczniowie z profilu biologicznego.
Na uzyskane wyniki, wpływ miał nie tylko profil edukacyjny. Stwierdzono istotny związek między wysokością stopni uzyskiwanych przez uczniów, a prowadzącym zajęcia. Średnie ocena uzyskiwana przez uczniów pani mgr Mediany to 2,83 przy odchyleniu 0,771, średnia ocena uczniów pani Chi Kwadrat to 3,9, przy odchyleniu 0,77. Rozkłady tych dwóch grup, różniły się też pod względem mediany i wynosiła ona odpowiednio 2,76 oraz 4. Tak jak w powyższym przykładzie posłużono się testem U, wynik okazał się istotny (z=-4,86, p=0,000). Uczniowie magister Chi Kwadrat uzyskiwali wyższe oceny.
Kolejnym czynnikiem, który miał wpływ na oceny z klasówki, były ogólne zdolności matematyczne ankietowanych. Jako wymiar tej zmiennej przyjęto końcowe oceny semestralne z matematyki. Ponieważ, obie zmienne znajdują się na skali rangowej posłużono się współczynnikiem korelacji Spearmana. Stwierdzono istotne korelacje między ocenami ze statystyki a ocenami z matematyki. Współczynnik r wynosił 0,784, przy poziomie istotności 0,000. Jest to silna korelacja dodatnia, uczniowie posiadający wysokie oceny z matematyki, lepiej przyswajali zagadnienia statystyczne.
Analizie statystycznej można poddać również zmienne jakościowe.
Sprawdzono stopień zrozumienia zagadnień statystycznych wśród licealistów. W poprzednich testach stwierdziliśmy, że uczniowie różnią się pod względem uzyskanych ocen. Uczniowie jednej z nauczycielek uzyskiwali wyższe wyniki. Niekoniecznie musi to świadczyć o lepszym opanowaniu materiału, może się okazać, że jedna z nauczycielek po prostu surowiej ocenia swoich uczniów. Dlatego zapytano się uczniów o stopień zrozumienia materiału. Zmienną grupującą była osoba nauczyciela. W tym celu skonstruowano tabelę krzyżową (tab.3).

Stwierdzono istotną zależność między osobą nauczyciela a stopniem opanowania zagadnień ze statystyki. Większość uczniów magister Anny Mediany nie potrafiło opanować materiału (33 obserwacje), w odróżnieniu od drugiego nauczyciela, który potrafił wyjaśniać w sposób bardziej zrozumiały (34 obserwacje). Związek jest istotny, wartość współczynnika Phi Yula wynosiła 0,667 przy poziomie istotności p=0,000. Wysoka wartość współczynnika świadczy o dość silnej zależności.
W analizowanym przykładzie, chcieliśmy zaprezentować najczęściej wykorzystywane przez nas metody statystyczne. Nie jest to oczywiście cały wachlarz naszych możliwości, właściwie każda analiza oraz ankieta jest inna i za każdym razem do danego problemu musimy podejść inaczej. Jeżeli są Państwo zainteresowani naszą ofertą, proszę o zapoznanie się z zakładką przebieg zlecenia.

